Understanding the Slope Intercept form is a crucial building block in Algebra 1, serving as a gateway to grasping linear equations and their graphical representations. This form, expressed as "y = mx + b," highlights two key components: the slope (m) and the y-intercept (b). The slope indicates the steepness of the line, dictating how much y changes for every unit increase in x, while the y-intercept reveals where the line crosses the y-axis. Recognizing these elements not only helps in solving equations but also enhances the ability to graph lines accurately. By converting different equations into this form, students can gain insight into the relationship between variables, making it easier to analyze trends and patterns. Furthermore, tasks such as graphing equations or deriving equations based on given parameters become more intuitive. Through practice and application, individuals can master this foundational aspect of algebra, laying the groundwork for more complex mathematical concepts in the future.
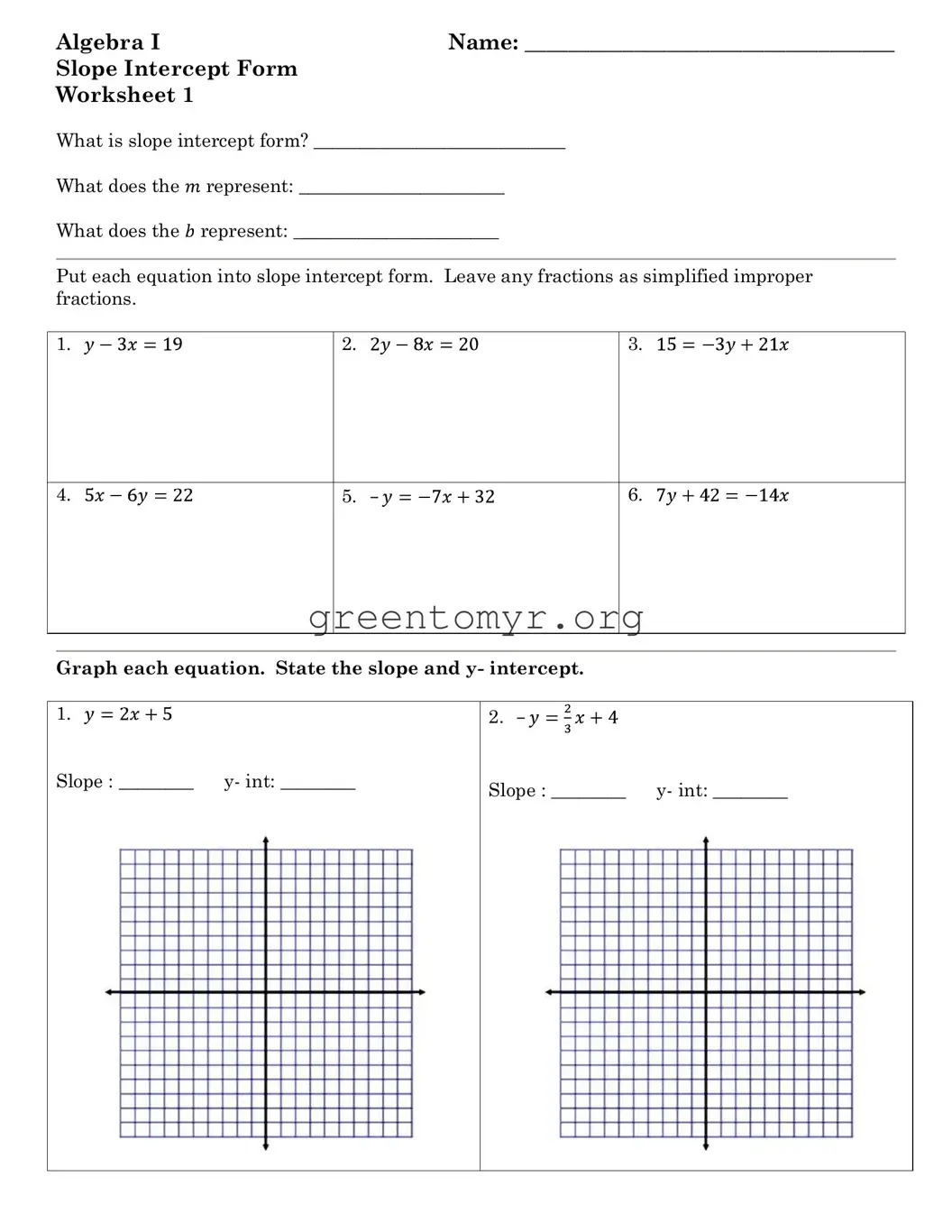
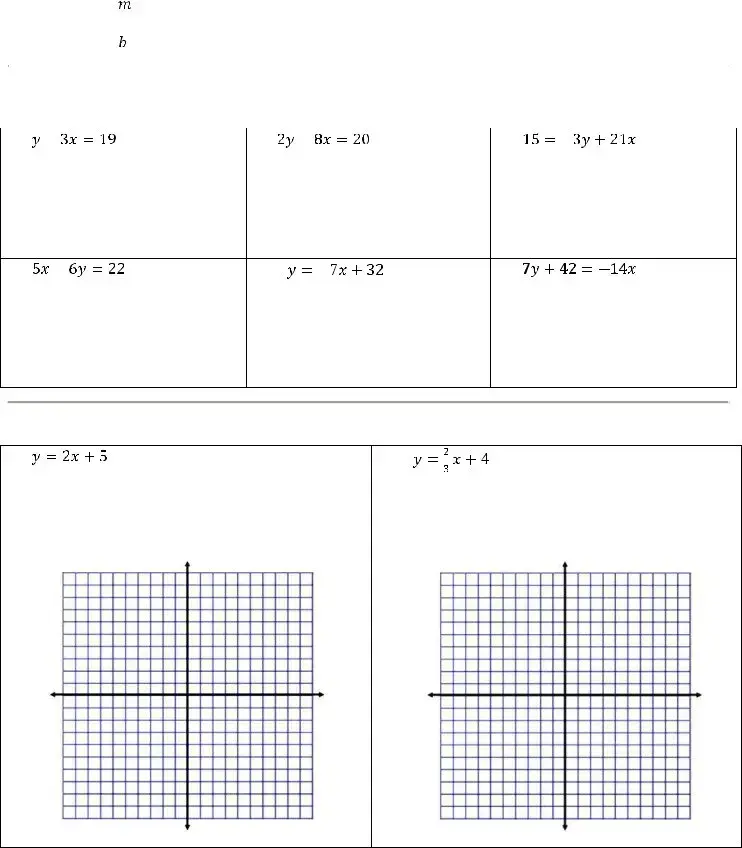
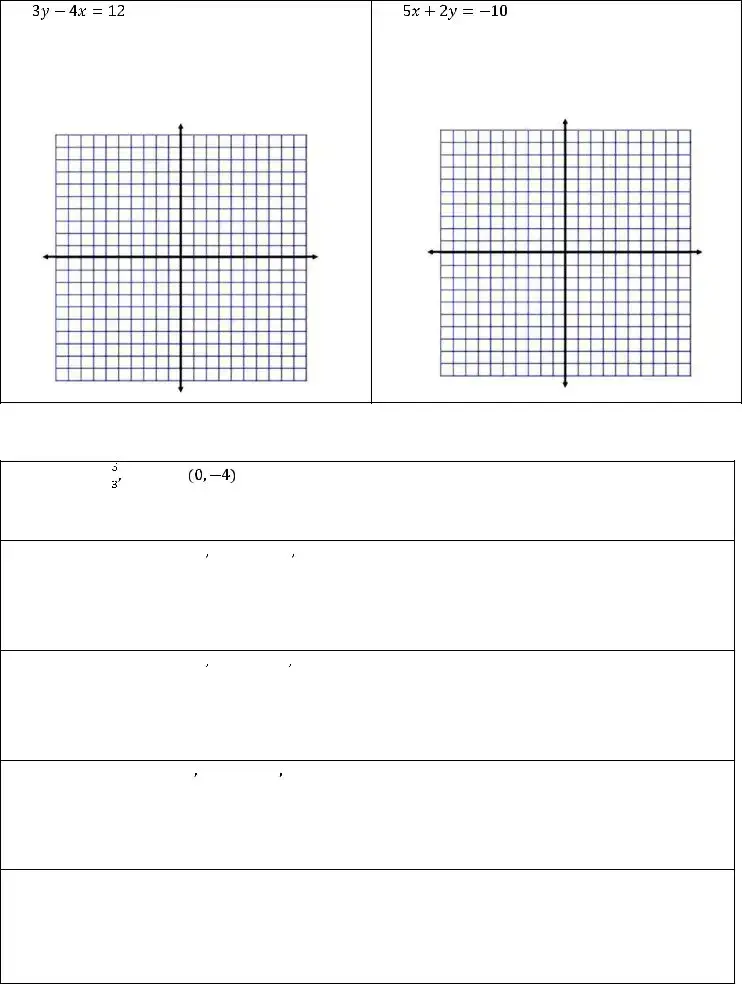




 and
and 





 and
and 





 and
and 






 and
and 


